P = Average pressure, psi
Figure 2 shows an experimental traction curve from Ref. 1 for counterformal elastohydrodynamic lubrication (EHL) as a function of the slide-to-roll ratio (SRR). It shows that the friction coefficient initially increases linearly from zero due to Newtonian behavior of the lubricant under low shear conditions (low SRR). However, this happens only within a very narrow range of SRR near zero SRR. As the SRR increases beyond about ±0.1, the shear stress within the lubricant film reaches the limiting shear strength of the non-Newtonian film. Beyond SRR = ±0.1, the friction coefficient typically decreases due to reduction of the limiting shear strength caused by temperature increase of the lubricant film in the contact zone resulting from heat generation in the film when sliding velocity becomes high.
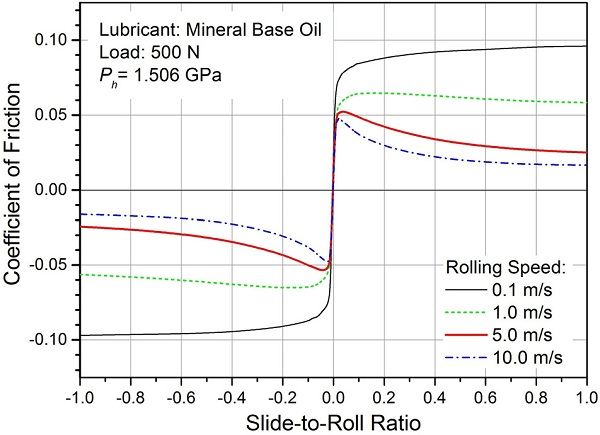Figure 2—Experimental traction curve for counterformal EHL contact (Ref. 1).
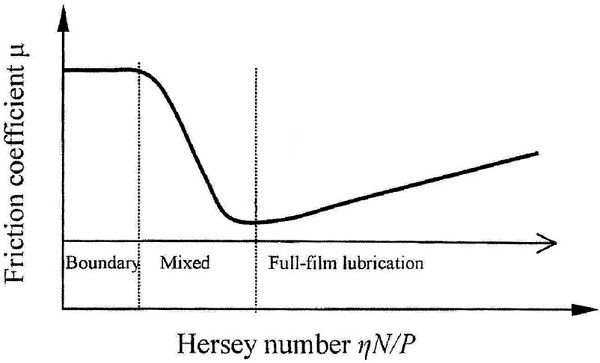
Figure 3 shows an experimental Stribeck curve from Ref. 1. Comparing Figures 1 and 3, it is evident that the friction behavior is similar in the boundary and mixed-film regimes, but very different in the full-film regime where the friction coefficient continuously decreases as the speed increases for counterformal contact (Figure 3), whereas the friction coefficient continuously increases for conformal contact (Figure 1). According to Ref. 1, the lubrication regime division lines in Figure 3 are approximate, and there is never a clear boundary between neighboring regimes (Ref. 1).
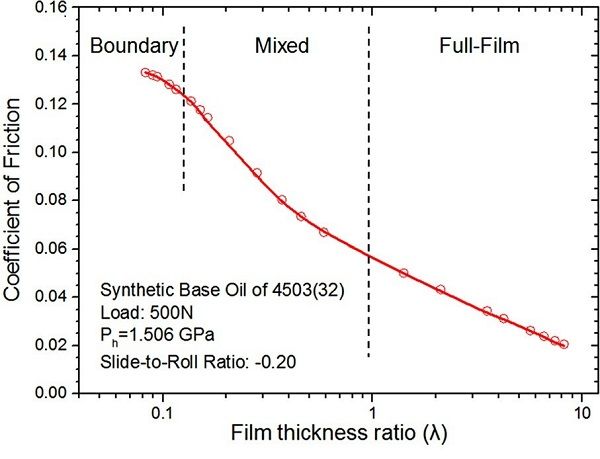Figure 3—Experimental Stribeck curve for counterformal contact ) (Ref. 1).
Discussion
The Stribeck curve was developed for journal bearings, which have conformal contact where the shaft journal conforms closely to the bearing bore. Under conformal contact, the peak contact pressure in a journal bearing is low (typically 5 MPa), film thickness is relatively high (typically 50 µm), and elastic deformation of the journal and bearing are insignificant. Under these conditions, the lubricant obeys Newton’s law of viscous flow.
In contrast, gears have counterformal contact, high contact pressure (typically 2,000 MPa, or 3 orders higher than a journal bearing), low film thickness (typically 0.5 µm, or 2 orders less than a journal bearing), and significant elastic deformations of the gear teeth. Under these conditions, the lubricant behaves as a pseudo-solid that exhibits non-Newtonian visco-elastic properties.
Consequently, to make the differences clear, it is best to refer to the operating regime of journal bearings as hydrodynamic lubrication (HL), and the operating regime of gears as elastohydrodynamic lubrication (EHL). Similarly, a Stribeck curve for journal bearings should show the regimes of boundary, mixed-film, and full-film HL, whereas a Stribeck curve for gears should show the regimes of boundary, mixed-film, and full-film EHL.
