How Reliable is a Reliability Calculation?

How Reliable is a Reliability Calculation?

Hanspeter Dinner

Objective of the Study

Figure 1: KISSsoft model used for calculation. Planetary carrier not shown; housing not shown.

Bearing failures are a major concern in wind turbine main gearboxes. The risk of bearing failure F(t) is calculated from the bearing life L. If this is done for all bearings in a gearbox, then, the bearing subsystem reliability for the required life R(H_req) = 1–F(H_req) may be calculated. Methods used for such calculations for wind gearboxes are well established and have been widely used in other fields, (Refs. 5–11).

A calculated failure risk will not necessarily reflect the failure rate experienced in the field. The reason for this is, e.g., that only a few failure modes are open to a reliability calculation. Here, another, sometimes overlooked reason, is addressed: The calculated reliability will change with any small variation of input parameters or calculation method.

Reliability as a Design Requirement for Wind Turbine Gearboxes

ISO 81400-4, (Ref. 1), states “…The required design life shall be specified for each of the major subsystems of the gearbox including gears, bearings, housings, shafts and seals….” In this statement, attention is directed to the underlying reliability of the material data or load capacity numbers associated with the life calculation of components. For the bearing rating, design rules (Refs. 1–3) usually stipulate a bearing failure probability of 10%. If in a gearbox each bearing reaches the required life H_req (e.g. 175,200 h = 20 y, using L_nmrh along (Ref. 4)) at a probability of failure of F = 10%, the reliability of the bearing subsystem is less than 90%. The reliability of the bearing subsystem is the product of all bearing reliabilities.

Single bearing reliability calculation. In B20 revision of AGMA 6006, (Ref. 2)), bearing reliability R(t) as a function of time t is calculated with a three parameter Weibull distribution:

Bearing Subsystem Life and Reliability

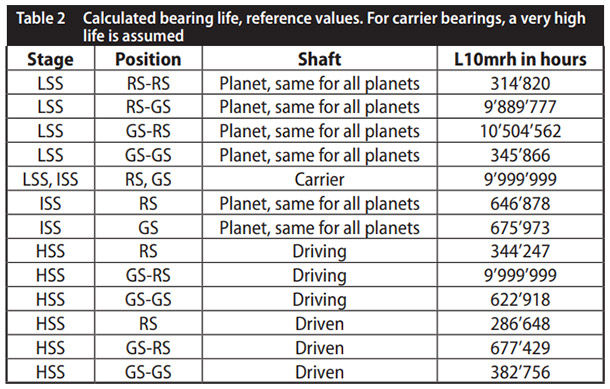
Base line model and reference conditions. The bearing subsystem of a 3MW class main gearbox is investigated. The rotor shaft is supported by two bearings; planet carrier bearing life is assumed as “infinite.”

Different effects are considered in the calculations. From a reference condition listed below, small changes are introduced to study how they affect the reliability of the bearing subsystem.

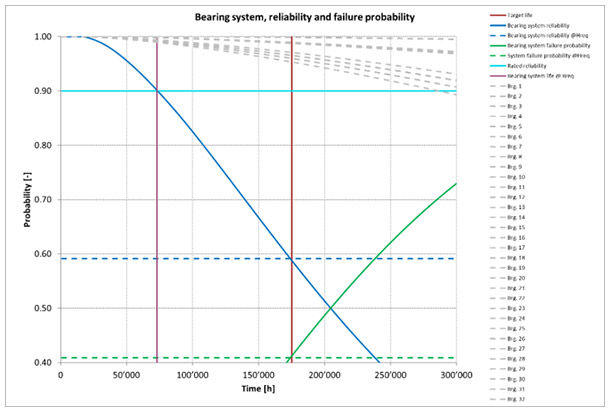
Bearings reliability (grey), subsystems reliability (blue), required subsystems life Hreq (vertical, red), rated reliability (horizontal, cyan), subsystem reliability at required life (horizontal, dashed blue), subsystem life at rated reliability (vertical, pink).

Results, reference calculation. With settings per DNV GL guideline (Ref. 3) and above, calculations are done using KISSsoft software (Ref. 1), giving:

For all 32 bearings, the reliability function R(t) is plotted (see figure 2 in grey). Bearing subsystem reliability (blue) is calculated therefrom. The intersection of subsystem life H_req at 175,200 hours (vertical, red) and the time dependent subsystem reliability (blue) results in a subsystem reliability value of about 0.59 (blue, dashed, horizontal line).

Variation of Calculation Settings

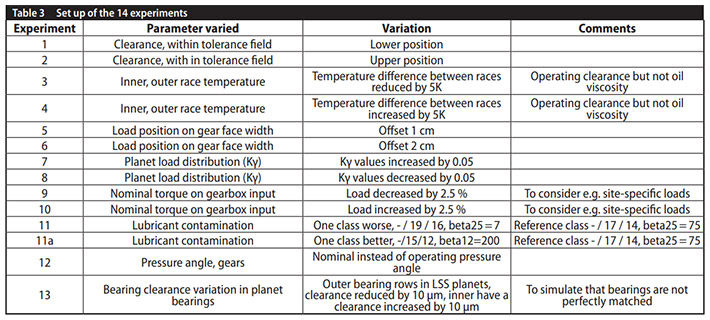
Parameters varied. Thirteen experiments are set up. Only one parameter is changed compared to the reference calculation.

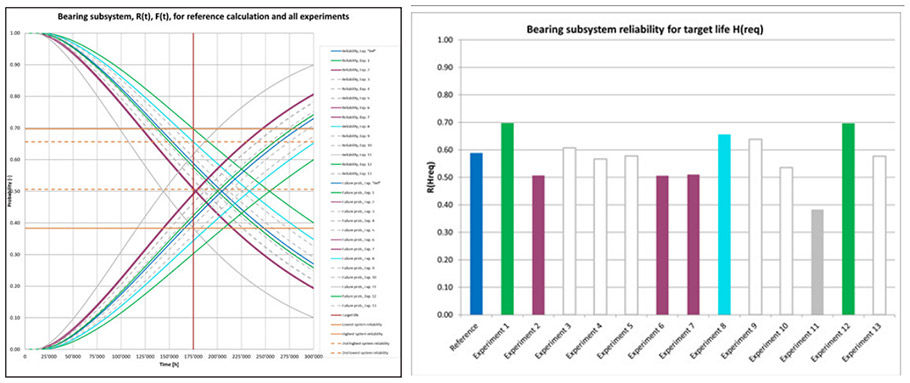
Resulting reliability curves. For each experiment, for all bearings, life and reliability curve are calculated. Bearing subsystem reliability and failure probability curve is plotted in (Figure 3). The resulting reliability values for the required life H_req are determined as intersection of the reliability curves with the vertical line at x = H_req. Experiment 1 and 12 gave highest reliability, highlighted (green). Experiment 8 gave second highest reliability (cyan). Experiment 2, 6 and 7 gave second-lowest reliability, (pink). Experiment 11 gave lowest reliability (grey, solid line).

Calculated reliability values R(H_req) range from 38% to 70%. If we accept that experiment 11 is extreme and omit it, we still find a range of 19%-points.

Conclusion

Governing effects. The reliability of the bearing subsystem is governed by the outer bearing rows in the LSS planet bearings and the output shaft bearings. We find that the biggest influence is from the lubricant cleanliness level. This is easy to understand as the lubricant cleanliness level itself affects the rated life of the LSS planet bearings the most, since those have the lowest lubricant film thickness and therefore a low aISO factor.

On the HSS bearings, a major influence is the pre-tension of paired TRBs and the influence of the bearing raceway temperature.

How reliable is the reliability calculation? We find that a calculated bearing subsystem reliability of a typical wind turbine gearbox has a typical error of ±10%-points.

If we are interested in comparing the total cost of ownership for several competing designs, based on bearing subsystem reliability numbers, this error of +/-10% is disappointing. The obvious solution is that all calculations must be done strictly with identical assumptions, calculation methods and tools.

Figure 3: Bearing subsystem reliability for different experiments (blue: reference calculation, green: highest result, pink: second lowest result, grey: lowest result, cyan: second highest results, white: other results). Upper image: reliability curves. Lower image: reliability levels at Hreq.

References

1. ISO 81400-4:2005. Wind turbines, Part 4, design and specifications of gearboxes.
2. ANSI-AGMA 6006-B20. Standard for Design and Specifications of Gearboxes for Wind Turbines, revision of ANSI/AGMA/AWEA 6006-A03.
3. Germanische Lloyd Rules and Guidelines Industrial Services. Guideline for the Certification of Wind Turbines, 2010.
4. ISO/TR 16281:2008. Rolling Bearings – Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings.
5. E. V. Zaretsky et al. Determination of Turboprop reduction Gearbox System Fatigue Life and Reliability, NASA/TM 2007-215019.
6. E. V. Zaretsky, Rolling Bearing Life Prediction, Theory, and Application, NASA/TP 2013-215305.
7. E. V. Zaretsky et al. Weibull-Based Design Methodology for Rotating Structures in Aircraft Engines, International Journal of Rotating Machinery, 9: 313-325, 2003.
8. M. Savage et al. Reliability Model for Planetary Gear Trains, NASA Technical Memorandum 82859, 1982.
9. D. G. Lewicki et al. Fatigue life analysis of a Turboprop Reduction Gearbox, NASA Technical Memorandum 87014, 1985.
10. Detroit Diesel Allison. Study of turboprop systems reliability and maintenance costs, NASA CR 135192, 1978.
11. M. Savage et al. Computerized life and reliability modelling for turboprop transmissions, NASA Technical Memorandum 100918, 1988.