Todd R. Bobak

Introduction
In the power transmission industry, shaft-mounted speed reducers provide one possible solution to meet the speed reduction/power generation needs for an application. As the name implies, a shaft-mounted speed reducer (SMSR) is a speed reducer mounted directly onto, and statically supported by, a driven shaft—the type of setup that may be found on a conveyor. Typically, the SMSR incorporates a hollow bore (with keyway, tapered bushing or some other coupling mechanism) to facilitate mounting onto the driven shaft.

The SMSR may be “fixed” to the machine using an output flange or, in certain instances, its housing may be bolted directly onto the machine. However, situations exist where direct attachment of the SMSR is either not possible or desirable. In such situations, the SMSR is supported only by the shaft that it is intended to drive. When the SMSR is mounted directly onto a driven shaft with no other external support, it must have a torque arm attached to it. A torque arm is a pivoted, connecting link between the reducer and a fixed anchor point intended to resist the torque developed by the reducer. Quite simply, a torque arm transmits the reaction torque produced by the SMSR into the structure of the machine, thereby preventing the counter-rotation of an SMSR during operation. Most manufacturers of shaft-mounted speed reducers have designed, and offer for purchase, standard torque arms for their products. Situations may exist, however, where a manufacturer’s torque arm does not meet the needs of a certain application (due to space limitations, for example). In such situations, the machine designer may be required to design his or her own torque arm to fit within the constraints of the application. This article provides some design guidelines for such a situation.

Resultant Force
In considering the design of a torque arm, first you need to understand the amount of load (or force) that the torque arm may see during unit operation. To determine this force, you need two pieces of critical information:

1. The torque capacity of the SMSR. As the name implies, this is the mechanical capacity (typically expressed in terms of inch-pounds or Newton-meters) that the SMSR is capable of developing at its output. While it may be tempting to simply multiply the motor output torque by the reducer’s reduction ratio to obtain an output torque value, it is recommended to consider (at a minimum) the larger of the following values: the SMSR’s output torque capacity (as listed in the product catalog) or, the product of the motor’s output torque and reduction ratio times an additional 2.5—to take into account the motor’s starting torque.

2. The dimensional location on the SMSR where the torque arm will be mounted. Manufacturers of shaft-mounted speed reducers provide at least one mounting location for a torque arm (Fig. 1). Note that the point where the torque arm attaches to the reducer (either directly or indirectly through a bracket) is known as the pivot point. Many manufacturers provide more than one potential location for the torque arm in order to accommodate the various mounting configurations available for a given product. The location(s) of these mounting holes/positions may be found in catalog cut sheets or through manufacturer supplied product drawings.

Figure 1—Manufacturers often provide multiple mounting holes for the placement of a torque arm, as seen in this picture of a Sumitomo Cyclo Bevel Buddybox.

Using Figure 1 as an example, let’s say an application requires a bracket-style torque arm, and this bracket will be attached to the housing at both identified mounting holes. Using the unit model size, reduction ratio, and motor input speed, you can determine the output torque capacity from the reducer catalog ratings table (Fig. 2).

Figure 2—Output torque capacity can be determined from a manufacturer’s spec sheet based on the model’s motor input speed rpm and gear reduction ratio.

You can also use the catalog dimension sheet to determine the location of the identified mounting holes relative to the center of the reducer’s output bore (Fig. 3).

Figure 3—Manufacturer’s specifications will also reveal the exact location of the mounting holes relative to the center of the reducer’s output bore.

With this information, you can now calculate the force acting at the selected pivot point, given the fact that torque is the product of force and distance. You can determine the unknown force (F) using these formulas:

It is important to note that during operation, the SMSR will tend to rotate about the driven shaft in the direction opposite to that of the driven shaft’s rotation. With this in mind, it is significant that the calculated force F (above) acts in pure tension on the torque arm. This fact is especially important for torque arms that are long—if they are exposed to compressive forces, they may buckle. Figure 4a shows the correct method of mounting a torque arm so that it is in tension.

Figure 4a—In order to maintain pure tension loading for the torque arm, the pivot point of the torque arm should run along, or parallel to, the line of action. The line of action (see figure 4b) is defined as the right angle formed by a line joining the pivot point and the center of the SMSR’s output bore.

Figure 4b—Determining the line of action.

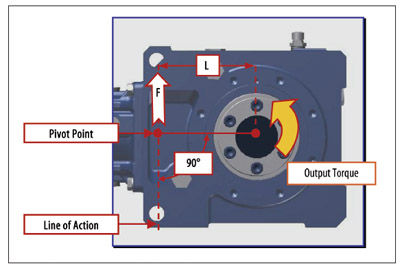
Using values from the manufacturer’s specifications (Figures 2 and 3 for our example), you can calculate the resultant force acting at the pivot point as follows:

In essence, the connection method at the pivot point you chose (i.e., bolt, threaded rod, etc.) must be able to withstand this calculated force when in tension. If you find that the calculated force exceeds the physical limits of the connection method, you may choose to incorporate a different, stronger material for the torque arm.

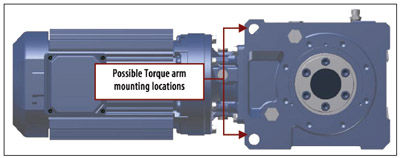
A way to minimize this force is to increase the distance L of the pivot point, as shown in Figures 5 and 6. In these examples, the reducer has a T-type torque arm mounted to it, which moves the pivot point an additional 1.85 inches farther from the center of the reducer’s bore.

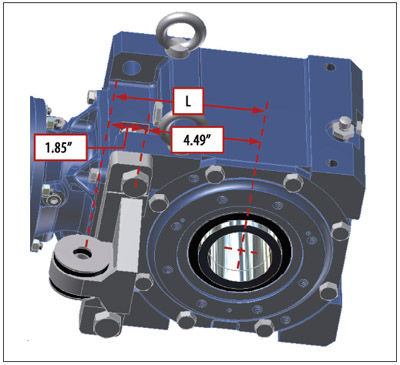
Figure 5—In this example, the reducer has a T-type torque arm mounted to Figure 5—In this example, the reducer has a T-type torque arm mounted to it, which moves the pivot point an additional 1.85 inches farther from the center of the reducer’s bore.

Figure 6—A shaft-mounted speed reducer in a conveyor application with a T-type torque arm.

If all other factors remain the same, this increase in distance yields a decrease of nearly 600 pounds in the force on the torque arm.

Thus:

Once again, this calculated force must be compared to the yield stress of the torque arm material to assure that the material limitations are not exceeded.

A Turnbuckle for a Torque Arm
Provided that it will fit within the design constraints of your application, you may opt to use a turnbuckle for a torque arm. A turnbuckle is a device commonly used to tighten a rod or rope. Its components include a sleeve with screwed connections of opposite hands (left and right) at each end. Upon turning the sleeve, the connected parts (threaded rods) will be drawn together, taking up slack and producing tension (Fig. 7).

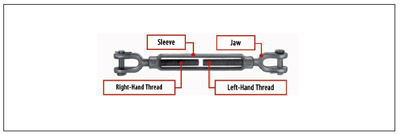
Figure 7—A typical turnbuckle.

You can calculate the force acting at the pivot point in this situation using the same formula for force as in the previous examples. Figures 8-9 show a typical mounting style for a turnbuckle torque arm.

Figure 8—A typical mounting style for a turnbuckle-style torque arm.

Figure 9—A turnbuckle-type torque arm being used on a Sumitomo helical shaft mount unit.

A Note About Mounting Hardware
In addition to assuring that the forces acting on the torque arm itself do no exceed the limitations of the torque arm material, you must also consider the effects of the force on the mounting hardware (nuts, bolts, etc.).

When taking this into account, you must note that the force is not acting on the hardware in tension, but rather in shear. Depending on the location of such hardware, bending movements induced by the force may also be acting on the hardware.

Hardware manufacturers usually provide yield and shear limitations for their products. Once again, it is important to compare the calculated forces/stresses acting on the hardware against the published limiting values to assure that the critical points are not exceeded.

A Note About Reversing Rotation
In reversing applications, the output of the SMSR rotates in one direction for a period of time, and then reverses and rotates in the opposite direction for a period of time. This application type requires considering the compressive forces that the torque arm must also bear.

Recalling that, ideally, a torque arm is mounted so it is in tension, in a reversing application, the torque arm may see a period of time when it also receives compressive forces. Such compressive forces, if great enough, could buckle the torque arm. For such applications, designers may want to add a second torque arm on the opposite side of the SMSR. The second torque arm would take the tension forces generated by the reverse rotation while minimizing the compressive forces on the first torque arm.

Angles Other Than 90°
Although it is important to maintain a pivot point at 90° to the center of the SMSR output hub, it may not always be possible due to limitations in the machine onto which the SMSR will be mounted. This is not uncommon, and reducer manufacturers who supply turnbuckle torque arms with their SMSR units often note that the torque arm may be mounted with an angular variation, such as ±15°.

In such situations, the designer needs to evaluate the effects of the resultant forces acting on the torque arm. Figure 10 shows a torque arm mounted to an SMSR at some angle (è) that is less than 90°.

Figure 10—A torque arm mounted to an SMSR at less than 90°.

Because the torque arm is not acting at a 90° angle to the output bore of the SMSR, there are two forces acting on it. The free-body diagram in Figure 11 details these forces.

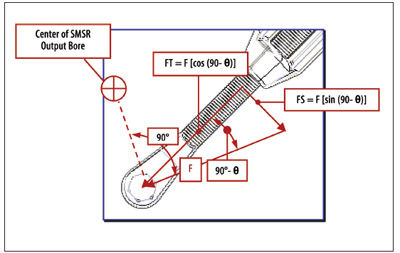
Figure 11—When a torque arm is mounted at an angle other than 90°, force F is composed of both tension (FT) and shear (FS) forces. Both must be considered when evaluating the strength of the torque arm design.

The resultant forces (FT and FS) are the component forces of Force “F” acting on the torque arm. These resultant forces place not only a force in tension (FT) acting on the torque arm, but also a shear force (FS). Both forces must be considered when evaluating the strength of the torque arm design.

The Effect of Shaft Runout
Despite a high degree of accuracy in manufacturing processes, shaft runout sometimes occurs. Such runout (on the driven shaft) may cause the reducer to “wobble” on the shaft during operation. This could be particularly troublesome if the torque arm is rigidly mounted to the anchor point. A rigidly mounted torque arm attached to an SMSR driving a shaft with a high degree of runout may result in (among other things) a broken driven shaft, cracks at the anchor point, a decrease in the life of the output bearings of the SMSR and/or the conveyor and lubrication leakage. Introducing some “float” in the torque arm at the anchor point will counteract these problems.

Float may be introduced at the pivot point by attaching rubber bushings to the pivot and anchor points, as shown in Figure 12.

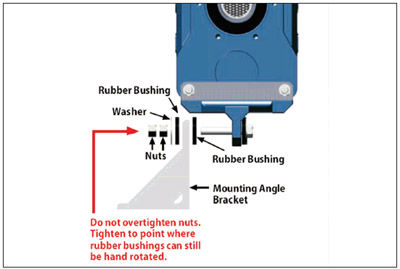
Figure 12—Rubber bushings installed at the anchor point and/or pivot point will provide “float” to compensate for runout in the driven shaft.

If dual rotation of the output shaft is possible in the application, manufacturers recommend installing rubber bushings on both sides of the pivot and anchor points so float is possible regardless of the direction of rotation.

A loose clearance designed between the bolts and through holes in the torque arm bracket may also assist in creating float.

In addition to taking precautions to eliminate a rigid mount, designers must also ensure the torque arm is properly aligned when mounting it to the SMSR. Misalignment may inadvertently cause binding that could decrease or entirely eliminate this float.

Conclusion
Although seemingly simple in concept, a torque arm is an important component when considering a shaft-mounted speed reducer for an application. Before selecting a potential torque arm design, designers should evaluate the offering supplied by the manufacturer of the shaft-mounted speed reducer. In doing so, they may determine that the standard offering fits into the application constraints. Additionally, some manufacturers offer more than one standard design (i.e., turnbuckle, T-type) to meet a variety of applications. However, if the existing available designs fail to meet the established application criteria, following the methodology detailed in this article will help to develop a functional and robust torque arm design.

Todd R. Bobak has worked in the gear industry for 15 years. He has held positions in technical service, design and development, and quality assurance. He is a product engineer for Sumitomo Drive Technologies in Chesapeake, VA.