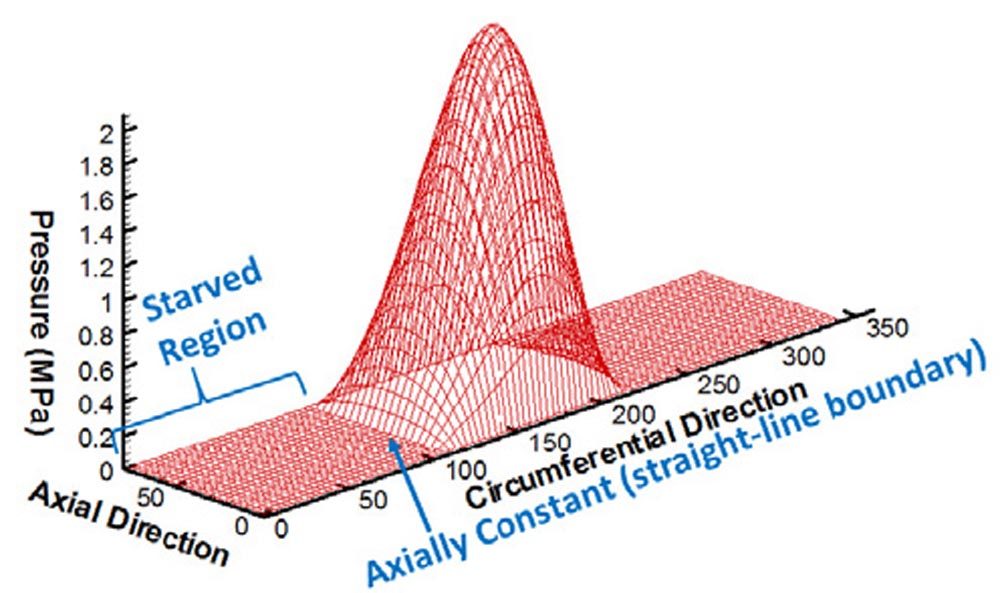
Figure 1—Starvation assumption of TEHD bearing codes used by He (Ref. 4).

Introduction

Fluid film bearings are used in a variety of turbomachinery to transmit loads from the rotating shaft to the stationary structure. Titling pad journal bearings support the radial loads and are used in a wide variety of machines due to their superior rotordynamic characteristics. Cavitation, starvation, and aeration are critical considerations in the physics of journal bearing performance as diverging regions of the film can cause cavitation or entrain air (Ref. 2). Starvation can also occur at the leading edge of the pad when the supply flow rate is insufficient to fill the gap between the journal and the pad (Ref. 5). Typically, Reynolds equation-based thermoelastohydrodynamic (TEHD) bearing codes assume that this starved region near the leading edge is axially constant (Ref. 4) as shown in Figure 1.

San Andres, et al. (Ref. 11) also use this leading-edge assumption in the prediction of low-frequency shaft motions. The basis for this assumption was the experimental results of Heshmat and Pinkus (Ref. 6) who tested journal bearings under a variety of flow conditions. Their results showed that streamlets form across the starved region of the film and that these streamlets coexist with the ambient air, producing no meaningful hydrodynamic pressure.

A byproduct of this starvation assumption is that pads opposite the loaded direction are likely to be predicted as fully starved before starvation is predicted in the loaded pads (Ref. 5). Lower hydrodynamic forces in the upper/unloaded pads suggest an increase in the film thickness on the loaded pads (Ref. 12). This prediction also suggests a significant change in bearing rotordynamic coefficients under starvation. Specifically, Whalen, et al. (Ref. 13) found dramatically reduced stiffness and damping coefficients under starved operating conditions. Starvation is also known to affect the performance of the bearing by reducing power loss (Ref. 3). Critically, reduced oil flow is also known to increase pad temperature (Brockwell 1997[QTA: No REF Info.?]).

Understanding flow starvation and correctly modeling it is therefore of great importance to the turbomachinery industry. This work evaluates the accuracy of the current starvation model popular in TEHD bearing codes and establishes shortcomings in the current theory that need to be addressed by those working in the field. The critical distinction that will be discussed in this work is that when a single large streamlet forms in a converging region of the film, hydrodynamic pressure can be generated. For this purpose of understanding the distributions of temperature, pressure, and phase during flow starvation, only the unloaded pad is discussed in this work.

Experimental Work

A series of heavily instrumented tilting pad journal bearing tests were performed by Kingsbury R&D in 2012. Select pads were fitted with arrays of probes to acquire more detailed information on the behavior of the individual pads. The tests provided unique insight into the complex behavior of the pads under various operating conditions. One behavior, in particular, was an indication of aeration at the axial edges of the pad in the case of insufficient lubricant flow rather than starvation at the leading edge which is a typical assumption in direct lube-bearing code development. The second key observation was that in the side-aerated state, the peak temperatures were measured on the axial edges of the pad rather than the trailing edge. Results are presented later in this paper. The simultaneous existence of side aeration and the increased temperature was difficult to envision until a recent CFD analysis of a slider bearing conducted by the University of Virginia predicted similar behavior.

Preliminary CFD Work

Preliminary work was done by the University of Virginia in 2016 on a slider CFD model with adiabatic wall conditions as shown in Figure 2. The question this model sought to answer was whether even with axially constant supply flow, starvation occurs following the straight-line assumption.

Figure 2—Slider bearing used for preliminary work.

In this model, oil was supplied in an axially constant supply opening as seen in the figure to allow for the best possible chance of matching the straight-line assumption. The boundary conditions are depicted in Figure 2, with the blue arrows showing the region of air ingestion as well as air and oil exit, the black arrows showing the oil supply, the red indicators showing symmetry, and the purple indicators showing the periodicity of the single pad model. Results for temperature and pressure for the unstarved case yielded predictable results. However, when the supply pressure was reduced, an increase in air volume fraction was observed at the axial edges of the pad rather than starvation at the leading edge as demonstrated in Figure 3.

Figure 3—Volume fraction on the groove and pad surfaces for starved slider bearing case (blue represents air and red represents oil).

Additionally, in this starved case, the temperature profile was unexpected. Figure 4 shows the temperature on the pad and groove surfaces.

Figure 4—Temperature distribution on the pad and groove surfaces under starved conditions. (blue represents cold oil and red represents hot oil).

The results indicated that the hottest point on the pad surface was not at the trailing edge of the pad, but instead at the axial edges. Similar CFD results for temperature and volume fraction were also recently reported by Sakai, et al. (Ref. 10) and Ochiai, et al. (Ref. 8) for a plain bore journal bearing. These results of peak temperature at or near the axial edge can be understood from the CFD models in terms of where the carried-over hot oil exits on the pad but was not known to be physical without the experimental correlations.

Objective of Study

Given the similarity of the experimental tilting pad test results and the preliminary slider-bearing CFD results, the authors agreed to collaborate on a joint project. The goal is to match the experimental tilting pad results with an exact CFD model to lay the groundwork for future studies explaining these phenomena of side aeration and peak temperature on starved pads.

The next two sections will describe the experimental and computational methodologies. Detailed comparisons of the results will then be presented. Finally, conclusions and future work will be discussed. Ultimately, it is desired that this project will form the basis for the development of more accurate TEHD bearing codes for starvation, aeration, and thermal modeling.

This study focuses exclusively on the unloaded pad (Pad 4 in Figure 5) due to having the greatest starvation. The CFD model was found to match broadly across all center-line temperature and pressure probe measurements. Discussion of these results will be the subject of future work as not to dilute the discussion of the unloaded pad and the relevant physical phenomena observed.

Experimental Methodology

Test Bearing

The test bearing is shown in Figure 5 and is described in Table 1.

Figure 5—The test bearing numbers indicate pad positions used throughout the paper.

Table 1—Test bearing geometry.

Select pads in the test bearing were fitted with arrays of probes to acquire detailed information on film thickness, film pressure, hydrodynamic film force, and pad temperature of the individual pads in the bearing. Although all pads have thermocouples, one in particular was instrumented with an array of fifteen thermocouples that allow construction of pad temperature isotherms. For simplicity, we refer to this pad as “Pad A.” The locations of these sensors are indicated in Figure 6.

Figure 6—Locations of temperature sensors in heavily instrumented Pad A. Direction of shaft rotation is left to right.  

 Another pad, which we call “Pad B,” was instrumented with five pressure transducers to record film pressure. The locations of these probes are indicated in Figure 7.

Figure 7—Locations of the five pressure probes (in blue) and nine thermocouples (in purple) in Pad B. Again, the direction of shaft rotation is left to right.

A third pad, “Pad C,” was instrumented with five capacitance probes and a load cell to capture film thickness and hydrodynamic film force. The locations of these are indicated in Figure 8.

Figure 8—Locations of the five capacitance probes (in blue), two thermocouples (in purple), and load cell (in the shoe support) in Pad C. Direction of shaft rotation is left to right in the schematic, and bottom to top in the lower left-hand picture.

The range and precision of the instruments used are given in Table 2.

Table 2—Description of instruments used.

For the first test in each series, the measured data include pad temperatures in position 1 from Pad A (Refer to Figure 5), film pressures in position 2 from Pad B, and film thicknesses and hydrodynamic load in position 5 from Pad C. After the first run, the bearing was physically rotated one pad position and the test was repeated. The second test yielded pad temperatures in position 5, film pressures in position 1, and film thicknesses and hydrodynamic load in position 4. This was repeated for a total of five tests so that each of the three specially instrumented pads (Pad A, Pad B, Pad C) were tested in all positions in the bearing at identical operating conditions. With temperature, pressure, hydrodynamic load, and film thickness data for each position, it is possible to examine all of the data at any of the pad positions for a particular set of operating conditions.

Test Cases

The results presented in this paper are limited to the conditions shown in Table 3 and focus solely on the unloaded pad position, pad position 4 in Figure 5. Plots of pressure, temperature, and film thickness acquired in these tests are presented later in side-by-side comparisons with the CFD results (Figures 11–16).

Table 3—Operating conditions of the test case.

CFD Methodology

CFD analysis was conducted at the University of Virginia using the computational cluster Rivanna and the commercial CFD software ANSYS CFX. Computational fluid dynamics solvers, like ANSYS CFX, solve the Reynolds-averaged Navier-Stokes (RANS) equations using numerical techniques such as finite element or finite volume methods. The computational model of the test setup is shown in Figure 9.

The model is half the bearing since axial asymmetric loading is negligible and therefore the model is symmetric about the centerline. This reduces the computational time by half. As can be seen in Figure 9, only a sliver of the full journal is modeled due to the periodicity applied at the circumferential edges. ANSYS CFX employs a “frozen rotor” option to then translate the sliver to a full cylindrical journal during computations. This allows for circumferential averaging of the temperature on the fluid side of the journal surface as it moves relative to the fluid. This is based on the assumption that due to the rotation of the shaft, the temperature on the shaft is axisymmetric. Conduction is modeled with a flux-conservative interface between all the solid and fluid components. The outside of the bearing shell is modeled as adiabatic.

Figure 9—Numerical model used in CFD analysis.

The surface speed of the rotor is applied as a no-slip wall at the fluid surface where it touches the journal. The fluid surface where it touches the pad is also no-slip, but stationary. A mass flow rate is specified at the supply to the supply annulus (top of the model) that corresponds to flow rates in Table 3. The end of the journal is modeled as adiabatic where it would connect with the rest of the shaft. The boundary conditions are depicted in Figure 9, with the blue arrows showing the region of air ingestion as well as air and oil exit, the black arrows showing the oil supply, the red indicators showing the symmetry, green dots showing the regions of connection between the solid and fluid surfaces, and the purple indicators showing the 2D periodicity of the journal. The thermal effects are modeled using the thermal energy model in ANSYS CFX and the problem was considered laminar as the Reynolds number is low. The multiphase problem is treated as homogeneous in both thermal and flow fields. Air is allowed to enter the bearing at the axial edges, which is modeled as incompressible air at 77°F (25°C). The convergence criteria, which is the root-mean-squared differential between the nodes of subsequent solutions in pressure, velocity, temperature, and phase were set to 1e-06. A conservation target, which measures the change in total quantities of mass, momentum, temperature, and phase between iterations, was specified as 0.01. The numerical scheme was high resolution.

Because the CFD model requires a film shape to be specified, but the known quantity in the experiment was load, Fluid-Structure Interaction (FSI) iteration was used to determine the correct loaded position of the journal and the pads. The FSI iteration was deemed to have converged when the load reached within five percent of the predicted load and the torque on the pads was less than 8.85 lbf-in (1 N-m). These criteria for force and moments were set based on further reductions in their magnitude not leading to meaningful changes in the eccentric position or pad tilt angles. Deformation of the pivot only was imported from a Reynolds equation–based TEHD solver. Deflection of the pads was ignored in the numerical analysis due to the relatively low bearing load.

Mesh independence was performed in both cases. Comparison of pressure, temperature, and volume fraction profiles for meshes of 0.360, 2.01, and 4.79 million elements were conducted. The results showed that the intermediate mesh had a sufficient number of elements. The mesh utilized is structured everywhere except the groove region to allow for fewer elements in the model. The mesh with 2.01 million elements is shown in Figure 10. The 2.01 million element mesh utilized 10 radial elements, and 0.0394 inch (1 mm) elements in the circumferential and axial directions.

Figure 10—Intermediate mesh density: (A) overall mesh; (B) fluid domain mesh; (C) mesh in the thin film.

Detailed results comparing the CFD based on the intermediate mesh and experimental data are presented in the next section.

Results and Discussion

Experimental results are given in part A of Figures 11–16. The unique data acquired regarding hydrodynamic film force, air volume fraction, oil film thickness, and pad temperature are represented by results for operating conditions stated in Table 3. Part B of Figures 11–16 show the corresponding CFD results. Note that shaft rotation in Figures 11 through 16 is right (leading edge) to left (trailing edge). The experimental plots shown in Figures 11–16 show a mix of interpolated and extrapolated values of the measured data. The interior white dots in these figures indicate sensor locations. The white dots on the periphery of Figures 11(A) and 14(A) indicate additional points at which we impose a zero-pressure boundary condition. Note that similar boundary conditions for film-thickness and temperature cannot be imposed on the peripheries of the pads in Figures 12(A), 14(A) and Figures 13(A), 16(A), respectively. We use the open-source visualization software ParaView (Ref. 1) to generate a two-dimensional Delaunay triangulation of the data. Values whose spatial coordinates fall inside the triangulation are interpolated and appear as surface plots in Figures 11–16. To extrapolate the experimental data exterior to the Delaunay triangulation, we construct a radial basis function fit to the data. The contour plots in Figures 11-16 are level surfaces of these fits. Finally, the color schemes in each plot were chosen to have agreement between surface and contour plots within a figure, and closely match the maximum and minimum values of the corresponding CFD simulation.

Figures 11 and 14 show a reduction in the pad pressure profile, correlating to a drop in hydrodynamic load on Position 4 from 1500 lbs to low levels as flow was reduced from 45 to 8 gal/min (2.83 to 0.505 l/s). (Hydrodynamic load is not shown in the figure.) Figures 11 and 14 also demonstrate a strong agreement between the experimental and numerical peak pressures with an error of about 3%. This error is likely due to the CFD’s iterative method for finding the correct loaded position. As stated above, the acceptable error in force was set to 5 percent, so a 3 percent error in peak pressure is very reasonable. The CFD results indicate a narrowing of the pressure profile axially as the supply flow rate is decreased. This is not as clearly observed in the experimental contours simply because the experimental pressure profiles were generated based on curve fitting the 5 pressure measurements and the outer most pressure sensor is 1.25 inches (0.0318 m) away from the axial edge. However, this trend is obviously consistent with the cavitation observed along the axial edges as indicated in Figure 15.

Figure 12 (A) indicates a reasonable film shape at 45 gal/min with a film thickness of 14 thousandths of an inch (0.3556 mm) at the leading edge, down to 3 thousandths of an inch (0.0762 mm) at the trailing edge. Figure 15 (A) requires some explanation. Capacitance probes were specifically chosen for film thickness measurements in these test series because their design depends on and is calibrated for the medium, in this case ISO VG 32 mineral oil. Should the medium change, the capacitance changes giving a false step change in measurement. Capacitance probes, therefore, become a suitable indicator for aeration.

Figure 15 (A) indicates a 0.012 in. (0.3048 mm) variation across the axial length of the pad which is physically impossible with the low load and temperature of this case. The butterfly shape is the result of a step change in measurement at the side detectors (Figure 7). In other words, the shape represents aeration of the oil at the location of the side detectors. That the step change appears to be smooth in Figure 15 (A) is a consequence of a finite amount of data points used in the plotting software. The center line film thickness, on the other hand, measures approximately eight-thousandths of an inch (0.2032 mm) at the leading edge and 6.5 thousandths of an inch (0.1651 mm) at the trailing edge, which is reasonable based on the clearances of the test bearing.

Given this indication of aeration at the axial edges, volume fraction (volume of oil to air) distributions on the side surface are shown in part B of Figures 12 and 15. Figure 12 (B) demonstrates low aeration, which is logical given the high supply flow rate. Small amounts of axial end leading edge aeration is observed. However, Figure 15 (B) shows that over half the pad surface has ingested air along both axial sides. The capacitance sensors on the axial edges are in this aerated region, thus explaining the butterfly-shaped film thickness in Figure 15 (A).

Part A of Figures 13 and 16 contain the measured pad temperature plots for the conditions under consideration. Figures 13 (B) and 16 (B) demonstrate close matches in the temperature across the pad between the CFD and experimental results within approximately 2°F (1.11°K) of the measurement temperature points. Figure 13, at 45 gal/min (2.83 l/s), displays isotherms typical of those expected and found in most technical papers, experimental and theoretical. Temperatures are low at the leading edge and increase in the direction of rotation toward the trailing edge of the pad. Figure 16 (A), on the other hand, displays maximum temperatures at the axial edges of the pad, a result that formerly seemed contrary to expectations of the pad temperature in a highly aerated region. Similarly, the CFD results depicted in Figure 16 (B) show that in the starved case, the highest temperatures exist at the axial edges. This is despite Figure 15 indicating the oil in this region is highly aerated.

Figure 11—45 gal/min (2.83 l/s) pressure results (psi) at position 4 (A) experimental (B) CFD.

Figure 12—45 gal/min (2.83 l/s) experimental film thickness results (mils) and CFD air volume fraction at position 4 (A) experimental (B) CFD.

Figure 13—45 gal/min (2.83 l/s) temperature results (F) at position 4 (A) experimental (B) CFD.

Figure 14—8 gal/min (2.83 l/s) pressure results (psi) at position 4 (A) experimental (B) CFD.

Figure 15—8 gal/min (2.83 l/s) experimental film thickness results (mils) and CFD air volume fraction at position 4 (A) experimental (B) CFD.

Figure 16—8 gal/min (2.83 l/s) temperature results (F) at position 4 (A) experimental (B) CFD.

Mechanisms of High Axial Edge Temperature During Starvation

A detailed review of the CFD results could provide an explanation as to why the highest temperature occurs in a highly aerated region. The work is beyond the scope of this paper, but a basic understanding involves the axial variation of the leading-edge oil temperature and the cross-film distribution of phase in the region.

First, the results show that, in the case of aeration, the cold supply oil stays centralized near the supply hole and the hot carried-over oil bifurcates to either side as can be envisioned in Figure 16 (B). Second, the cross-film distribution of phase in the aerated regions shows a higher volume fraction at the pad surface. This runs counter to the theoretical understanding that the oil adheres predominately to the shaft in cavitated regions (Ref. 2). However, the CFD results include centrifugal force, which forces the oil towards the pad surfaces at the high-speed operating conditions under consideration. In other words, the hot oil is flowing over the pad surface in this region. Therefore, the hot oil carry-over from the previous, more loaded, pad is producing the high axial edge temperatures observed in both CFD and experimental results. If the pad were adiabatic, the temperature would be fairly constant along the axial edges, but conduction through the pad from the center moderately cools the sides of the leading edge.

With these two mechanisms in mind, experimental observation of high axial edge temperatures can be envisioned as hot carried-over oil convecting to the pad surface and heating it along the side edges. It is the authors’ intention to present the mechanisms of high axial edge temperature during starvation in more detail in future publications.

Conclusions

A series of heavily instrumented tilting pad journal bearing tests were performed by Kingsbury R&D where select pads were fitted with arrays of probes to acquire more detailed information on the behavior of the individual pads. The effort was in response to industry challenges regarding the accurate prediction of bearing performance and vibration characteristics.

A computational fluid dynamics (CFD) analysis of the test was conducted at the University of Virginia using the computational cluster, Rivanna, and the commercial CFD software, ANSYS CFX.

This paper compares the results of a CFD model with experimental data for an unloaded pad in a directed lube journal bearing under regular and low oil supply flow conditions. The nominal flow case is used to calibrate the CFD model. In the low flow condition, both the experimental data and the CFD model exhibit the same two phenomena: first, the axial edges of the journal pad in question aerate on the axial edges rather than cavitate at the leading edge; and second, the hottest pad temperatures move from the trailing edge of the pad to these aerated regions on the axial edges. These results can be used to evaluate the accuracy of current starvation models popular in TEHD bearing codes and allow for the development of more accurate codes regarding starvation and thermal modeling. Critically, it was found that under flow starvation, the unloaded pad produced a single large streamlet with meaningful hydrodynamic pressure, which is currently unaccounted for in most TEHD bearing codes.

Future Work

This paper focused solely on the unloaded pad of a certain test bearing. Data exists for all pad positions, so the next step is to correlate the performance of the other pad positions and operating conditions.

The complete series of tests also investigated other parameters such as load-on-pad and load-between-pad orientations, steel and chrome copper pad materials, oil distribution configurations, and evacuated vs flooded housing configurations. Future correlation of experiment vs. CFD models will be useful in distinguishing the influence of such parameters and others. For example, the complete series of tests were performed for a 1.0 length-to-diameter ratio bearing. A validated model would better allow a prediction of how shorter L/D bearings affect the cavitation and temperature characteristics.

Future work also intends to further demonstrate the cause of these phenomena through systematic CFD analysis and determine the conditions under which they occur. This will aid in the development of an improved Reynolds equation TEHD bearing code that will better predict film shape and temperature, thus providing better overall performance predictions.

Long term, it is the authors’ objective that the observations and modeling of the phenomena presented in this study will lead to more accurate prediction of bearing performance and vibration characteristics, enabling the industry to design better, more efficient, and safer turbomachinery.

Acknowledgments

The authors would like to acknowledge the financial support of the Rotating Machinery and Controls (ROMAC) consortium and thank Kingsbury, Inc. for their tests and permission to present the associated results. The authors also thank Dr. Seckin Gokaltun for his invaluable assistance and Dr. Luis San Andrés for his critical review and input. Scan DeCamillo passed away in February 2021 after completing his portion of this paper. Our thoughts are with Scan’s family.

References

1. Ayachit, Utkarsh, 2020, “The ParaView Guide Community Edition,” http://www.paraview.org, Kitware Inc.
2. Brewe, David E., J. H. Ball, and Mansour Mohammadian Khonsari, 1990, "Current research in cavitating fluid films," NASA STI/Recon Technical Report N 90, 28791.
3. Brockwell, K., Dmochowski, W., DeCamillo, S., 1994, “Analysis and Testing Of The Leg Tilting Pad Journal Bearing-A New Design For Increasing Load Capacity, Reducing Operating Temperatures And Conserving Energy,” Proceedings of the 23^rd Turbomachinry Symposium, Turbomachinery Laboratory, Texas A&M University, College Station, Texas, pp. 43–56.
4. He, M., 2003, “Thermoelastohydrodynamic Analysis of Fluid Film Journal Bearings,” Ph.D. Dissertation, University of Virginia, Charlottesville, VA.
5. He, Minhui, Cloud, C.H., Byrne, J.M., Vázquez, J.A., 2016, “Fundamentals of fluid film journal bearing operation and modeling,” Proceedings of the Asia Turbomachinery & Pump Symposium, Turbomachinery Laboratory, Texas A&M University, College Station, Texas, pp. 155–176.
6. Heshmat, H., Pinkus, O., 1985 “Performance of Starved Journal Bearings With Oil Ring lubrication,” J. Trib., Vol. 107, No. 1, pp. 23–31.
7. Heshmat, H., 1991, “The Mechanism of Cavitation in Hydrodynamic Lubrication,” Tribology Transactions, Vol. 34, pp. 177–186.
8. Ochiai, M., Sakai, F., Hashimoto, H., 2019, “Reproducibility of Gaseous Phase Area on Journal Bearing Utilizing Multi-Phase Flow CFD Analysis under Flooded and Starved Lubrication Conditions,” Lubricants, Vol. 7, No. 9, p. 74.
9. Rotta, G., Wasilczuk, M., 2007, "CFD analysis of the lubricant flow in the supply groove of a hydrodynamic thrust bearing pad." Proceedings of the ASME/STLE 2007 International Joint Tribology Conference. ASME/STLE 2007 International Joint Tribology Conference, Parts A and B, San Diego, California, pp. 307–309.
10. Sakai, F., Ochiai, M., Hashimoto, H., 2017,, “CFD Analysis of Journal Bearing with Oil Supply Groove Considering Two-Phase Flow.” Proceedings of the 4th International Conference on Design Engineering and Science, ICDES, Japan Society for Design Engineering, Tokyo, p. 131.
11. San Andrés, L., Koo, B., Hemmi, M., 2017, “A Flow Starvation Model for Tilting Pad Journal Bearings and Evaluation of Frequency Response Functions: a Contribution Towards Understanding the Onset of Low Frequency Shaft Motions,” J. Eng. Gas Turbines Power, Vol. 140, No. 5: 052506 (14 pages).
12. Tanaka, M., 1991, “Thermohydrodynamic performance of a tilting pad journal bearing with spot lubrication.” J. Trib., Vol. 113, No. 3, pp. 615–619.
13. Whalen, J., Cerny, V., Polreich, V., He, M., 2015, “The Effect of Starvation on the Dynamic Properties of Tilting Pad Journal Bearings.” Proceedings of the 44th Turbomachinery & Pump Symposium. Turbomachinery Laboratory, Texas A&M University, College Station, Texas, pp. 1–10.