Field Weakening—What, How, and Why to do It

Don Labriola P.E.

Let’s start with why field weakening is useful: it produces a wider speed range for a motor — with a constant torque at lower speeds and an almost constant power capability at higher speeds. This technique increases the motor power capability while also improving efficiency. There are many papers and patents discussing how to implement and optimize field weakening.

A synchronous motor produces a back-EMF proportional to the shaft speed of the motor and the strength of the magnetic field in the motor gap (field strength). A high torque constant motor also has a high back-EMF constant. (If the torque constant is in Nm/A , and the voltage constant is in V/Radian/Sec — the two constants are equal if losses are not included in the measurements).

Older motors and generators with a separate field winding could directly control the field strength and thus the back-EMF. Figure 1 (US2,925,550) shows how the field strength is intentionally adjusted to cause the resulting current to have a leading or lagging phase angle. The leading phase angle occurs when the motor is over-excited (back-EMF exceeds line voltage) and appears to be a capacitive load at the terminal frequency. The lagging phase angle occurs when the motor is under-excited, and appears to be an inductive load at the terminal frequency. This is the method used by a “synchronous condenser” used to adjust the VAR (Volts Amps Reactive) to improve the power factor (and reduce the power company charges) for larger factories.

Figure 1: from US8866423B2.

But how does this get us to field weakening if we are using permanent magnets? Adjusting the phase of the drive current can allow the motor to be operated from a drive voltage that is less than the back-EMF of the motor. If there is magnetic material between the magnet and the gap, the intervening magnetic material can be made to oppose the magnetic field from the permanent magnet. The permanent magnet is not weakened, but the magnetic field in the gap of the motor may be reduced. This reduces both the torque constant and the voltage constant of the motor. The current is often characterized by the torque producing in phase current (Id) and the weakening quadrature current (Iq), which may also be viewed as the current magnitude and phase. The peak current must be limited due to driver (inverter) ratings and motor heating.

To give a real example, the QuickSilver Controls SilverMax X34HC-2 motor has a back-EMF constant of 0.98 v/Radian/Second. At 500 rpm => 8.33 Rev/Sec => 52.36 Radians/Sec, the voltage across the terminals is 36.5 v peak. The motor torque curves show operation to 2,500 rpm with a 48 v DC supply, and almost 400 W mechanical output power. The open terminal back-EMF of the motor is some 136 v peak at 2,500 rpm! Without field weakening, this motor would be limited to approximately 880 rpm with a 48 v power supply and would have a much reduced torque at that speed.

Motor types: PMSM vs IPMSM: Permanent Magnet Synchronous Motor versus Interior Permanent Magnet Synchronous motor.

There are many variations of synchronous motor designs, but a common dividing line is whether the rotor magnets are directly facing the airgap to the stator or whether the magnets are mounted interior to the rotor with the flux directed to the gap through a highly permeable magnetic material. There are several factors that favor each of these designs. The surface mount magnets (Fig. 2) can minimize the inertia of the rotor, allowing for faster acceleration, and can offer simpler design for smaller motors. However, as the speeds and diameters increase, significant efforts may be necessary to affix the magnets to the rotor against the high acceleration; this is made more difficult when the adhesives must operate over wide temperature ranges. The servo motors typical of these face-mounted magnets typically have a fairly constant torque curve, but they only develop their maximum power near their maximum speed. Operation at half-speed will result in only half-power, and low speeds will show significantly lower efficiencies.

Interior permanent magnet synchronous motors were designed to overcome several of these issues. There are multiple approaches here as well, from the internal permanent magnet transverse flux motor (Fig. 4) to various low-pole-count rotor structures with interior magnets (Fig. 3). Common to the interior (or internal or buried) permanent magnet designs are: 1) generally a reduction in the volume of magnet material needed, 2) added mechanical structure to support/protect the magnets, and 3) the ability to employ field weakening. Most designs also include the ability to improve low-speed torque by use of variable reluctance of the rotor in addition to the torque produced using the permanent magnets. (Fig. 3).

Figure 2: Face magnets

Figure 3: IPMSM US9,792,760.

Figure 4 shows another form of internal permanent synchronous motor. When used open loop these are called step motors; used closed loop they are hybrid servo motors. The permanent magnet is placed between the two rotor caps, which each have 50 teeth in this example.

Figure 4: Internal permanent magnet transverse flux synchronous motor.

The ability to weaken the magnetic field for high-speed operation is used to significantly extend the power and efficiency curves of the motor. This improved performance has caused IPMSM motors to be increasingly used for improving efficiency — especially when used over a wide range of speeds.

In most of the articles and papers describing field weakening, the current is considered as an in-phase (I) and a quadrature-phase (Q) component. These are both oriented to the back-EMF generated by the windings on the stator when the rotor is rotated.

Field Weakening

Figure 5: Motor end view.

For 3-phase motors, the physical currents are electrically 120 degrees apart, so they must be transformed to equivalent I and Q. For 2-phase hybrid servo motors (transverse flux synchronous motors), the physical currents are 90 degrees apart, so visualizing the effects of the I and Q currents is somewhat easier. When rotating, the two physical currents would need to also be combined into I and Q components, as the rotor rotates with respect to the stator. Again to simplify, the figures will show the rotor positioned so that the rotor angle is aligned with the stator such that the black windings represent the in-phase component (I), while the red windings are the quadrature component (Q). Again, this is only true for the instant in time that the rotor and stator have this alignment. The rest of the angles require transforming the physical currents into their I and Q components. Still, the snapshot in time is useful for visualization.

Figure 5 shows and end view of the motor. The arrows at the 9:00 position are just to show the rotor-stator alignment at this moment in time.

Figure 6 shows a permanent magnet located between the blue pole cap and the grey pole cap.

Figure 7 shows that the teeth in the blue pole cap are aligned with the gaps in the grey pole cap.

Figure 6: Rotor side view.

Figure 7: Rotor close up oblique..

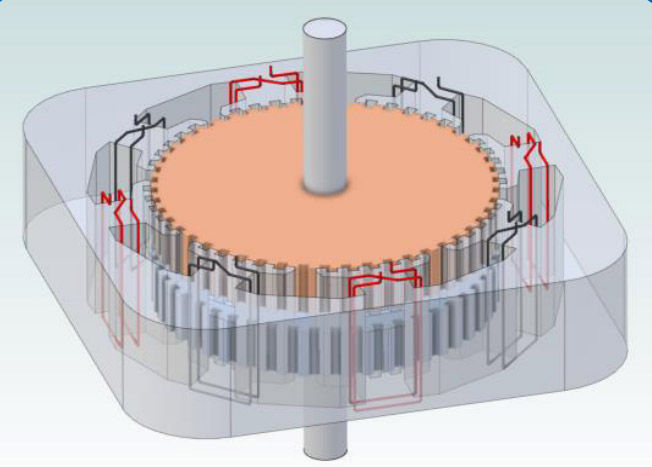
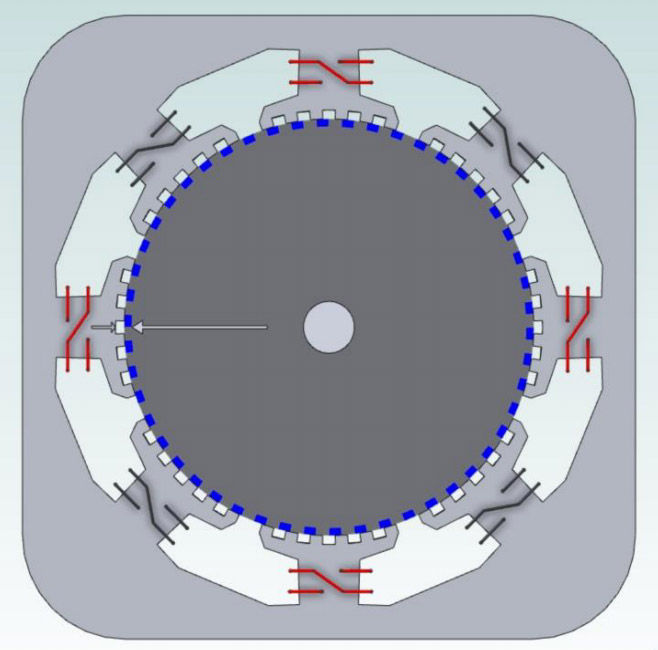
The windings at the top and bottom (12:00, 6:00) are both of the same phasing, i.e.— a positive current will cause the teeth of these phases to attract the north pole of the rotor, while those at the right and left sides have the windings connected in the reverse sense, and so will attract the south pole of the rotor. If the magnet inside the rotor (Fig. 6) is oriented so that the grey rotor cap is N and the blue rotor cap is S, then a positive current through the red windings will attract the grey teeth at 12:00 and 6:00 and while repelling the blue teeth. At 3:00 and 9:00 the stator windings have the opposite winding sense as at 12:00 and 6:00, so they will repel the grey teeth and attract the blue teeth; the result is a clockwise torque production. We will call the red windings “Phase A.”

The four black windings on the diagonal stator poles, which we will call “Phase B,” for this given rotor to stator alignment, have teeth that are balanced with respect to the rotor teeth. Energizing this Phase B in either direction will not produce torque between the stator and the rotor. Let us assume that the stator poles at 1:30 position (upper right) and at the 7:30 position (lower left) attract a north pole when energized with a positive current, while those at 4:30 (lower right) and at 10:30 (upper left) are wound in the opposite sense and will attract a south pole when energized. One can see the teeth at 1:30 and at 7:30 are mostly coupled to the blue (south pole) of rotor, while those at 4:30 and 10:30 are best coupled to the grey (north pole). Thus energizing the B-Phase while the rotor is at this position will either aid the magnet field of the rotor (is the teeth have a net field that is of the same polarity as the permanent magnet — repelling the rotor teeth), or will buck some of the magnetic field of the permanent magnet if they have the opposite polarity (i.e. attracted) to the rotor end caps.

For this instant in time that the rotor has this position, the A-phase is acting as the torque- producing quadrature phase, while the B-phase produces no torque, but can be used to strengthen or weaken the effective field strength at the rotor teeth (gap) — which is the function of the In-phase component of the driving currents.

The function of A and B reverse their roles when the motor advances 1.8 degrees mechanical, as the teeth B-phase stator poles will now be in greatest misalignment to the rotor, while those of the A-phase will be symmetrical to the rotor teeth. The I (in-phase) and Q (quadrature) components of the drive currents, must then follow the rotation of the rotor as the motor is commutated, so the static position example given for phase A and phase B at the one given position is only useful at that one position. But the same torque producing and field strengthening or weakening does apply for I and Q components as the motor is rotating.

Hopefully this gives a good physical interpretation of how field weakening occurs in a motor with an interior magnet. If the magnets are on the face of the rotor, there is not carrying of the flux from the in-phase drive component of the stator field, as the permeability of a fully charged magnet is nearly the same as air (that is, its b-h curve is saturated and the addition of additional field strength from the electromagnets of the stator are unable to significantly change the flux through the rotor magnet(s).

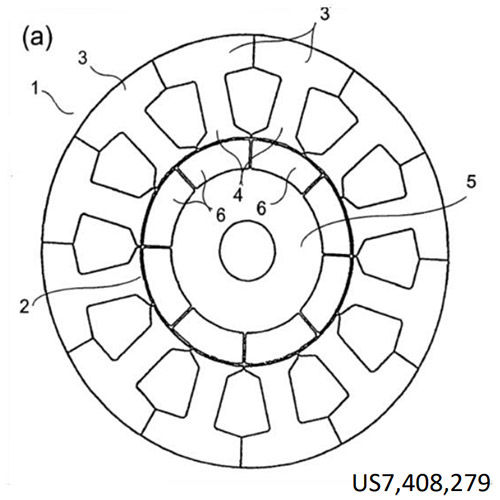
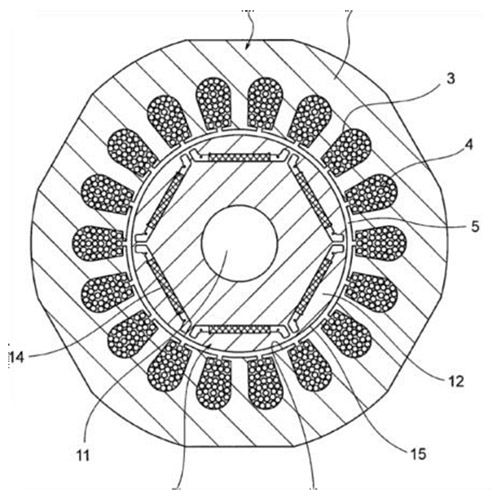
The interior permanent magnet motor design of Figure 3 also has variable reluctance coupling (saliency) between the stator and the rotor, due to the gaps and structure within the rotor, and has similar ability to do flux weakening, although it may be a bit more difficult to visualize in this structure as compared to the transverse flux design. The face-mounted magnet or Figure 2 does not have this saliency or variable reluctance; there is no high permeability magnetic material between the magnet and gap to allow flux to be captured and redirected from the I-phase component areas to the Q-phase torque-producing portions, and so this motor with face magnets is not normally able to be field weakened.

But Why Weaken the Field?

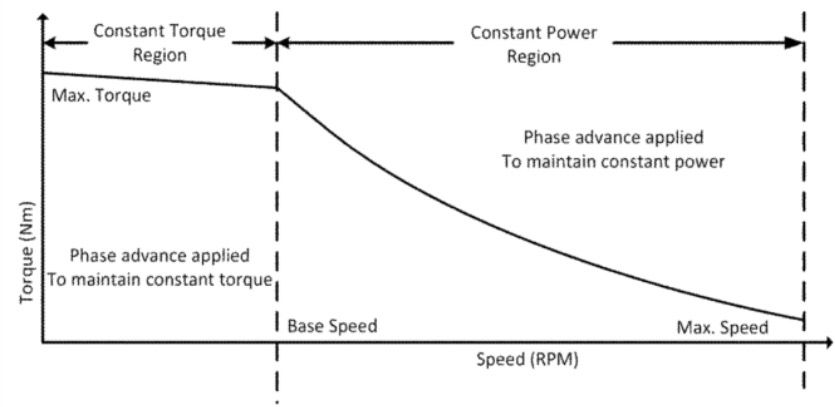
The motor generates back-EMF when the motor is in motion. The magnitude of the back-EMF is proportional to the strength of the magnetic field across the gap and the speed of the motor. The maximum speed of the motor is limited by the ability of the driver to force current into the motor windings. As the motor speed increases, the back EMF increases, and would eventually exceed the driver supply voltage. Using field weakening, the strength of gap field can be reduced, which reduces the back-EMF for a given speed. The lower back-EMF constant (torque constant) caused by the field weakening thus allows the motor to be run at a higher speed. Typically, this can double available motor speed.

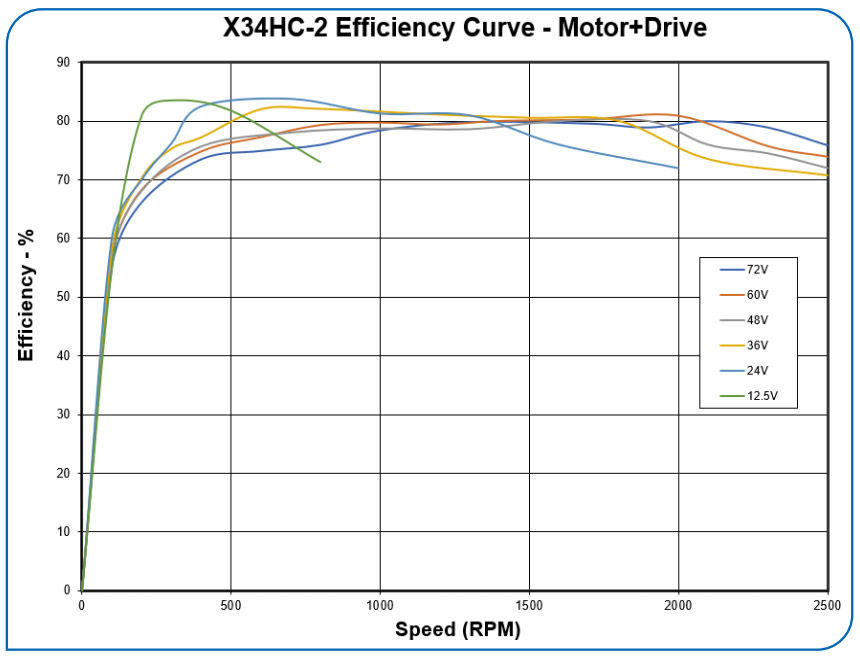
The mechanical power available at the output of the motor (including the losses from friction and windage) is the back-EMF times the quadrature portion of the winding current (cross product to be more exact). The main copper loss is the current squared times the resistance. Thus, for a given current, the best efficiency comes when the back-EMF is as large as possible as compared to the resistive I-R drop. Having the ability to vary the field strength allows the back-EMF to be kept near the maximum (power supply voltage) over a fairly wide range of speeds, which allows the motor efficiency to remain fairly high over a fairly wide range of speeds. Figure 8 shows how the efficiency can be kept high over a wide range of speeds and over a wide range of voltages. The curves show the measured combined efficiency of the motor and the driver.

Figure 8: Speedrpm.

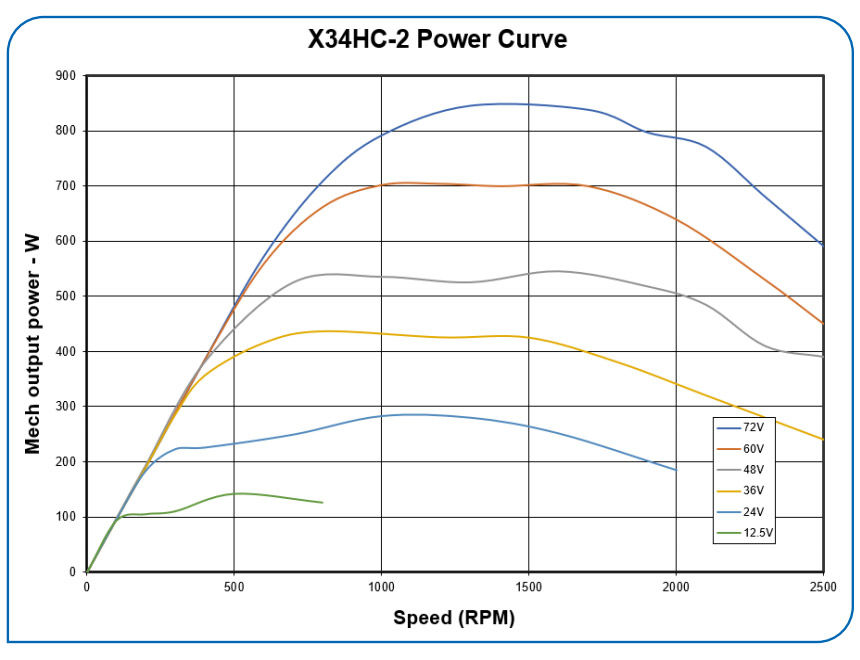
The field weakening also extends the available power curve, keeping the available power nearly constant over a two-to-one speed ratio, as seen in Figure 9. The higher available voltage allows for higher output power levels, as would be expected.

Figure 9: Speedrpm.

Hopefully this article has helped improve the understanding of how field weakening may be implemented in indirect permanent magnet motors — including hybrid servo motors — and why it is beneficial.